文章地址:https://www.usenix.org/system/files/conference/usenixsecurity17/sec17-wang-tianhao.pdf
标题:Locally Differentially private Protocols for Frequency Estimation
作者:Tianhao Wang, Jeremiah Blocki, and Ninghui Li
发表会议:USENIX Security Symposium 2017
Introduction
DP已经成为隐私保护的一大主要法则。已经有很多方法在DP的背景下提出。其中之一就是频率估计。首先用户将自己的数据进行编码,编码之后再随机化,然后将随机化的数据发送给集成者,集成者通过收到的数据对频率进行估计。
本文引入了一个 pure-LDP 的分析框架,现有的很多方法都可以被融入到这个框架之中。同时本文也分析了其他方法的优缺点,并且改进了其他的方法。
总的来说,本文的贡献点如下:
- 引入了 pure-LDP 的分析框架
- 我们引入了 Optimized Local Hashing,可以有效降低估计误差
Background and Existing Protocols
DP的提出假定有一个可信的数据管理者(data curator),他从用户那里收集数据并以一种满足DP的方式处理数据并公布处理的结果。因此DP希望一条记录的变动对整个处理结果影响不大,通过这种方式DP保护了这一条记录的隐私。DP的定义如下:
An algorithm $\mathbf{A}$ satisfies $\epsilon$-differential privacy if and only if for any datasets $D$ and $D’$ that differ in one element, we have:
where Range(A) denotes the set of all possible outputs of algorithm A.
Local Differential Privacy Protocols
LDP的概念就不重复阐述了,在 LDP 框架下,一般数据收集-分析的过程包含以下几个步骤:
- Encode:用户将自己的数据进行编码。
- Perturb:对编码之后的数据进行扰动处理,使其满足LDP的需求。
- Aggregate:集成者通过收集的数据对频率进行估计。
那么频率估计如何去描述呢,我们可以假定有 $n$ 个用户,每个用户 $j$ 有一个值 $v^j$,其中,用户值的范围为 $[d] = \{1,2,…,d\}$。频率估计的任务就是统计每个数据对应的频率。当前来说有着一些方法可以进行频率估计。
Basic RAPPOR
RAPPOR来自谷歌那篇《RAPPOR》论文,我们先讲一下Basic RAPPOR,这个编码过分为以下几步:
Encoding: $B_0 = Encode(v)$,这一步也叫做 Unary Encoding,其实就是对于一个数字 $v$,编码到一个 $d$ 维的数据,其中第 $v$ 位为1。假如 $d=5, v=1$,那么编码的结果就是 $[0, 1, 0, 0, 0]$。
Perturbation-1:替代的过程又分为了两步进行,分别是永久替代(Permanent randomized response)和即时替代(Instantaneour randomized response)。永久替代的过程就是对上一步的结果 $B_0$ 中的每一位进行基本的Random Response,得到 $B_1$,方法如下:
- Perturbation-2:即时替代就是对于上一步永久替代的结果,根据其每一位比特的值在进行一步替代,如果是1的话以概率 $p$ 为 1,如果是0的话以概率 $q$ 为1,在RAPPOR的实现中,满足 $p=0.75, q=0.25$。
- Aggregation:替代的数据发送给服务器之后服务器需要进行一个计数操作,即收到所有的数据,我们看每一位对应的位上有多少个1,然后再估计原始数据的频率,估计的方法如下:
以上就是 Basic RAPPOR 算法了,其对用户的带宽和计算cost为 $\Theta(d)$,对于aggregator来说为$\Theta(nd)$。在隐私上,其可以保证的隐私程度为 $\epsilon=\ln \left(\left(\frac{1-\frac{1}{2} f}{\frac{1}{2} f}\right)^{2}\right)$。(注意这里没有考虑即时替代)
RAPPOR
在RAPPOR中,最多只能出现 $d$ 种不同的数据,当数据很多的时候,这种方式就存在一定的问题,所以这里有一种更通用的编码方法了,还是分为几步:
- Encoding:每个用户有 $m$ 个哈希函数,表示为:$\mathbb{H}=\left\{H_{1}, H_{2}, \ldots, H_{m}\right\}$。这些哈希函数的输出都在 0 和 $k-1$ 之间,即 $H(v)\in [k]$。然后编码的过程就是将原始数据编码到一个 $k$ 长度的比特串中(其实这里就是一个bloom filter)。
- Perturbation:和Basic RAPPOR一样,用perturbation过程。
- Aggregation:由于哈希函数的使用,这个统计的过程有着一定的不确定性,需要用回归去大致估计了。
对于RAPPOR来说,其用户端的计算和带宽消耗为 $\Theta(k)$,Aggregator的不好具体去计算,因为需要用到Lasso回归。当然,这个cost肯定比 Basic RAPPOR高。其隐私保证为 $\epsilon = \ln \left(\left(\frac{1-\frac{1}{2} f}{\frac{1}{2} f}\right)^{2 m}\right)$,其实就是因为每个用户编码的比特串中有 $m$ 个1,所以总的隐私保证就是上面这个公式了。
Random Matrix Projection
这个方法目前还未接触,本文也未进行分析对比,就先不进行介绍了。
A Framework for LDP Protocols
首先,现在那么多的LDP方案,有没有一个统一的框架来去描述不同的方法呢?为了统一不同的方案,作者提出了 pure LDP 的概念。在介绍什么事 pure LDP 之前,我们现需要了解 $Support$ 的概念。作者是这么描述 $Support$ 的:
The function $Support$ maps each possible output $y$ to a set of input values that $y$ supports.
举个例子,在 basic RAPPOR 中,一个向量 $B$ 对应的是其第 $i$ 位为1的值,比如[0,0,1,0,0,0]对应的是2。即 $Support(y)=x$ 表示的是哪些x经过编码之后变成 $y$。定义了 $Support$ 概念之后,我们就可以介绍什么是 pure LDP了。
给定编码机制 $PE(x) = Perturb(Encode(x))$ 和 $Support$ ,一个机制是 pure LDP 的,如果存在概率 $p^*>q^*$ 使得对于所有的数据 $v_1$:
这个公式实际上意味着在概率映射当中只存在两个概率,高概率和低概率。对于RAPPOR来说,它就不是pure LDP的。那么对于一个pure LDP的机制来说,我们就可以根据下面的公式去计算原始的值的频数:
上面这个公式也是比较显然的。有了频数,就可以去计算频率了。作者在定理1中证明了这个对频率的估计是无偏估计,由于证明过程太显而易见了,这个证明就不作总结了。
相对于无偏估计,有时候我们更希望去计算出方差,在 pure LDP 中,下面的公式可以计算出对数据频数估计的方差:
在很多应用场景中,大多数数据的频率较低,当频率很低时,上面的方差可以用以下公式代替计算:
同时,当 $p^{*}+q^{*}=1$的时候,上式也成立。
有了上面的基础之后,我们就可以统一地去分析很多LDP机制了。
Optimizing LDP Protocols
根据前面提到的 pure LDP 概念,很多方法是满足这个东西的,本文考虑了以下几种方法:
- Direct Encoding (DE): 这种方法就是不编码,直接用 random response。
- Histogram Encoding (HE): 这种方式将数据以直方图的形式表示,分为两类:
- Summation with Histogram Encoding (SHE)。
- Thresholding with Histogram Encoding (THE)。
- Unary Encoding (UE): 把一个数据 $v$ 编码到长度为 $d$ 的向量中,使得 $v$ 对应的位为1。然后进行替代,替代中两个参数很重要 :$p$ 表示1变到1的概率, $q$ 表示0变到1的概率。
- Symmetric Unary Encoding (SUE): SUE中,$p+q=1$,即Basic RAPPOR这种编码方法。
- Optimized Unary Encoding (OUE): OUE中,更好地去设计 $p$ 和 $q$,这是本文提出的方法。
- Local hashing (LH),分为两类:
- Binary Local Hashing (BLH): 二元输出的LH。
- Optimized Local Hashing (OLH): 优化之后的LH。
Direct Encoding (DE)
DE实际上就是k-RR,只不过其用向量表示输出结果而已。在DE中,每个值编码之后对应一个向量,并且向量中仅有1位为1。其过程为:
- Encoding and Perturbing:首先编码,然后替代,可用以下方法表示:
很显然,这个过程是满足 $\epsilon$-LDP 的。
- Aggregation:对于DE来说,其 $\text { Support }_{\mathrm{DE}}(i)=\{i\}$,而且这个过程是 pure的,对应的参数为 $p^*=p, q^*=q$,根据前面的方差结果,其方差为:
那么DE有什么问题呢,其实问题还是挺大的,尤其是当数据空间比较大的时候,比如 $d = 2^{16}, epsilon = \ln 49$,这时候,数据保持和自己一样的概率是 $\frac{49}{65484} \approx 0.00075$,这个概率实在是太低了,会导致数据误差很大。
Histogram Encoding (HE)
在直方图编码中(Histogram Encoding, HE),输入值 $x \in [d]$ 被编码到一个 $d$ 维的比特串中。大概需要以下两个过程:
- Encoding:$\text { Encode}_{\text{HE}}(v)=[0.0,0.0, \cdots, 1.0, \cdots, 0.0]$。因为不同的编码结果的L1距离为2,所以接下来添加的噪声为2。
- Perturbing:$\text{Perturbe}_{\text{HE}}(B)$ 输出$B’$,其中 $B’[i]=B[i] + \text{Lap}(\frac{2}{\epsilon})$。
定理4是用来证明 HE 满足 $\epsilon$-LDP 的。证明的过程相当于组合性质,证明的过程如下:对于输入 $v_1, v_2$ 和输出 $B$,有:
用户发送完了数据之后,就到了Aggregator进行集成了。
- Aggregation: Summation with Histogram Encoding(SHE)。这个过程其实很简单,就是收集了数据之后把所有的行加起来得到一个 $d$ 维的求和结果。即:$\tilde{c}_{\mathrm{SHE}}(i)=\sum_{j} B^{j}[i]$,其中 $j$ 表示第 $j$ 个用户。对于SHE来说,这个方法没有 $Support$ 函数,同时也不是 pure-LDP的。很显然,这个估计是无偏估计的。
定理5说这个方法的方差为:
其中,拉普拉斯的噪声就是 $8/\epsilon^2$,然后一共有 $n$ 个用户,就得到了上式的方差了。
- Aggregation: Thresholding with Histogram Encoding (THE)。
Unary Encoding (UE)
接下来,我们看这个Unary Encoding,这也是我觉得用处比较多的一种编码方法。
- Encoding: $\operatorname{Encode}(v)=[0, \cdots, 0,1,0, \cdots, 0]$。首先把一个数据编码到一个 $d$ 维向量,其中数据对应的那一位为1,其他为0。这种方法也可以理解为 one-hot encoding。
- Perturbing: $B’ = \operatorname{Perturb}(B)$,其中概率转换为:
那么很显然,这个方法是提供 $\epsilon$-LDP 的,其中:
这也就是定理6给出的结论,证明过程其实很简单。
- Aggregation: 对于Aggregation来说,其$\text { Support }_{\mathrm{UE}}(B)=\{i | B[i]=1\}$,也就是在pure-LDP中,有 $p^*=p, q^*=q$,所以这个方法的方差为:
其中,利用 $\epsilon$ 的公式可以将 $p$ 转换成 $q$,这样就只有一个参数了。
- Symmetric UE (SUE): 这实际上就是对称的情况,即 $p+q=1$,那就等价于 $p = \frac{e^{\varepsilon / 2}}{e^{\varepsilon / 2}+1}, q=\frac{1}{e^{\varepsilon / 2}+1}$,这种情况下,方差的表达式为:
其实 $p+q=1$ 是最容易想到的方法了,那么这种方法是否最优呢,实际上并不是,其实还可以有更优的方案,也就是接下来要提的 OUE 方法。
- Optimized UE (OUE): 更优的方法意味着更小的方差,所以我们对方差求偏导就可以,即
根据这,就可以推导出:$p = \frac{1}{2}, q = \frac{1}{e^\epsilon+1}$,这时候,方差为:
这个Optimized方法挺有意思的。
Binary Local Hashing (BLH)
这篇文章中介绍 local hashing 说可以提高 RAPPOR 的表现,我没有怎么 get 到。不过我觉得这个技术是需要和其他技术结合起来的。看了下局部敏感哈希的介绍,好像有点懂这个东西怎么用了,以后再待细致挖掘。BLH 的输出只有 0 和 1,也就是这个 Binary 表示的意思。所以对于哈希函数簇来说,需要满足这样的条件:
实际上,按照我对这里的哈希函数的需求来说,小于1/2虽然是必要的,但是应该要小于一个更小的值。再给了这样的哈希函数簇后,我们看一下编码解码的过程:
- Encoding. $\operatorname{Encode_{BLH}}(v)=\langle H, b\rangle$,其中 $H$ 是一个满足上述要求的哈希函数,且 $b=H(v)$。也就是说,我们是这么编码一个数据的:选定一个哈希函数,然后用这个哈希函数及哈希函数的结果去表示这个数据。这里提到哈希函数可以建立索引,如果有 $n$ 个用户的话,那么索引只需要 $O(\log n)$ bits。
- Perturbing. $ \text { Perturb }_{\mathrm{BLH}}(\langle H, b\rangle)=\left\langle H, b^{\prime}\right\rangle$就是替代的过程了。其中替代过程为:
- Aggregation. 这里其实没有分析Aggregation的过程,不过我们可以分析一下support函数,为:$\text { Support }_{\mathrm{BLH}}(\langle H, b\rangle)=\{v | H(v)=b\}$,对应的参数为 $p^*=p, q^*=\frac{1}{2}p+\frac{1}{2}q=1$,所以方差为:
目前这里是怎么个 Aggregation ,我还没完全搞明白。
Optimal Local Hashing (OLH)
按照 BLH 的思路,为什么输出一定是 0 或 1这个 binary 的数据呢?咱也可以说有 $g$ 个输出呗,不过 BLH是 $g=2$ 的情况,所以哈希函数的要求现在是:
- Encoding. $\text { Encode }(v)=\langle H, x\rangle$,这个过程和原来是一样的。
- Perturbing. $\text { Perturb }(\langle H, x\rangle)=(\langle H, y\rangle)$,由于现在有 $g$ 个输出了,所以需要这么处理
定理7说这个过程是满足LDP的,这点当然是很显然的,就不分析了。
- Aggregation. 同样我们看一下支持函数:$\text { Support }_{\mathrm{LH}}(\langle H, y\rangle)=\{i | H(i)=y\}$。这时候的参数为:
对应的方差为:
同样的,为了求出最优的 $g$ 我们求导就好了:
即,参数为:$g=e^{\varepsilon}+1, p^{*}=\frac{1}{2}, q^{*}=\frac{1}{e^\epsilon+1}$,对应的方差为:
不过,这里有问题啊,因为 $g$ 肯定只能取整数的,这个分析并不能给出 $g$ 应该怎么取值,也不能说明 $g$ 取 $e^\epsilon+1$ 取整就是最优的。
后面又将 OLH 和 OUE 做了一个简短的分析,这个分析结果也体现在后面的 communication cost 中。
Which Protocol to Use
那么前面说了那么多种不同的方法,具体到应用中应该如何选择呢?表1列出了不同方法的 cost 和方差

同时表2和图1给出了不同 $\epsilon$ 下方差的具体数值。

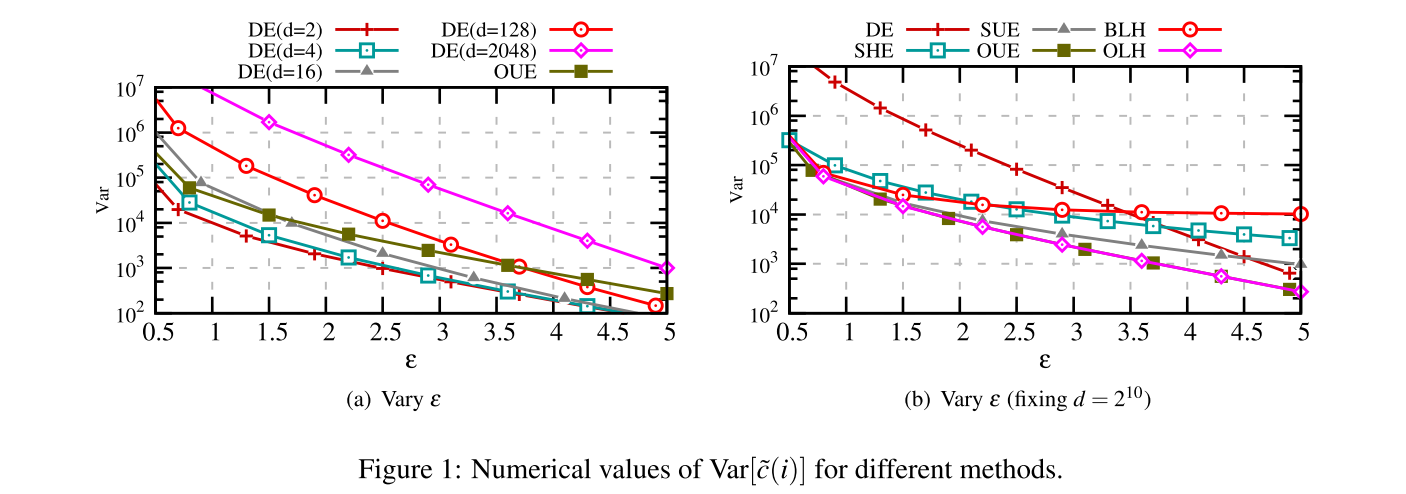
因此作者给了这么一些 guidelines:
- 当 $d$ 很小的时候,即 $d < 3e^\epsilon+2$ 时,DE是所有方法中最好的方法。
- 当 $d > 3e^\epsilon+2$时候并且 $\operatorname{cost}=\Theta(d)$ 是可接受的时候,这时候更推荐OUE,因为 OUE 和 OLH 的房差一样,但是 OUE 更容易实施,而且更快,因为 OUE 并未使用哈希函数。
- 当 $d$ 太大导致 $\operatorname{cost}=\Theta(d)$ 不太可以接受的时候,我们应当使用 OLH,因为OLH 和 OUE 提供了一样的方差,并且 cost 为 $O(\log d)$ ,比 OUE 的 $O(d)$ 要小很多。
Experimental Evaluation
接下来我们看一下不同的方法的实际表现,每个实验结果平均运行了十次。
Verifying Correctness of Analysis

在图2的数据中,作者首先生成了一个虚拟的数据集,是Zipf分布,限定了10000个用户,同时每个用户的数据范围为 $d$,误差是这么衡量的:$\frac{1}{d} \sum_{i \in[d]}\left[\tilde{c}(i)-n f_{i}\right]^{2}$,也就是用的平均平方误差。图2的结果很明显,就不介绍了(值得注意的是,$g=e^\epsilon+1$,取得最近的整数)。
Towards Real-world Estimation
我们再看一下真实的数据集,就是为了考虑这些方法在真实环境下的表现。其中数据集采用的是 Kosarak 数据集,这个数据集含有 80亿条对41270个不同网页的点击。
Accuracy on Frequent Values
其实我们之前说过,现在的估计在低频率的数据估计上是恨不准确的。所以这里是先估计,然后对最高频率的30个频率进行误差估计。因为其他的频率都很低,如果统计所有条目的频率的话,可能不太准确。
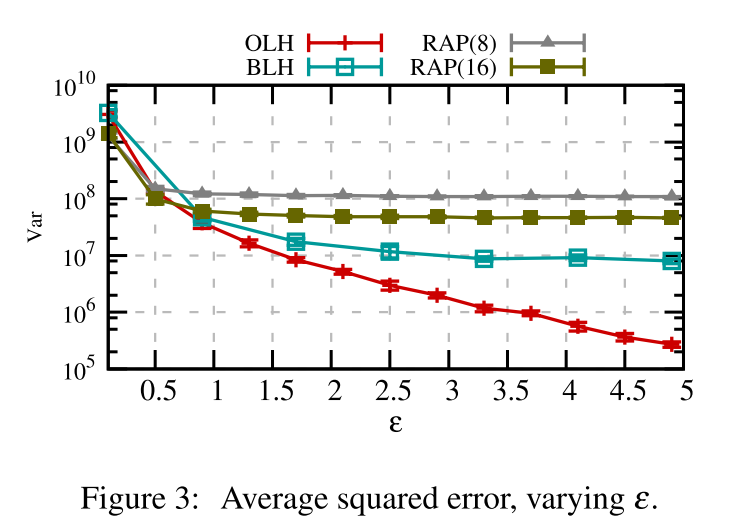
实验结论就是当 $\epsilon>1$ 的时候,OLH 优势开始体现出来,同时OLH的方差降低的更快。由于 bloom filter 的使用,当 epsilon 比较大的时候 RAPPOR 表现的并不是很好。
Distinguish True Counts from Noise
在估计的结果中,对于频率低的数据,估计的结果中我们无法看出来是由于噪声的加入使得估计的频率低还是原来频率低导致频率低,即不好判断噪声对低频数据的影响。
Significance Threshold. 在论文13中,作者给出了一个阈值,高于这个阈值的结果被保留,低于这个阈值的认为估计就不可信了,这个阈值为:
其中 $d$ 是数据范围,$\Phi^{-1}$ 表示标准正态分布累计密度函数的逆,$\alpha$ 本文选定的是 $\alpha=0.05$。

Number of Reliable Estimation. 图4展示了不同 $T_s$ 下的 True Positive,即你认为频率高于 0.05的数据估计的频率也高于0.05,因为 $\epsilon$ 的变化会影响 $T_s$,所以横坐标直接选定的 $\epsilon$。结论是对于 RAPPOR 来说, cohort 对 TP 影响不大,BLH 效果也不太好。
On Information Quality Now
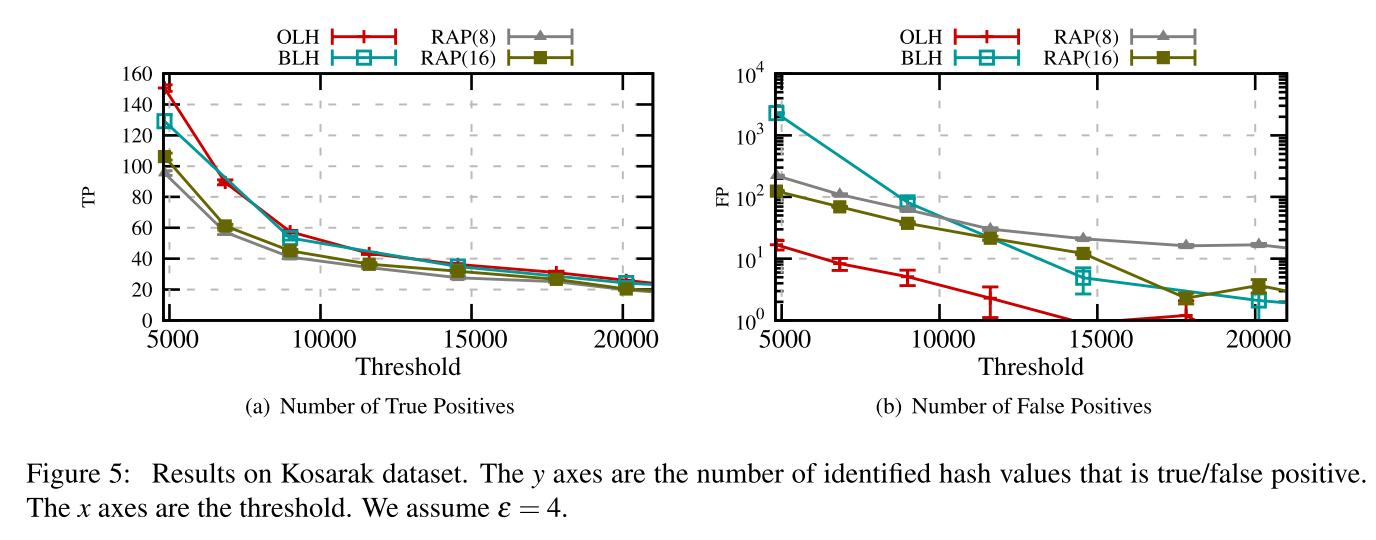
这里又继续看了 $T_s$ 对 TP 和 FP 的影响。总的来说,OLH 还是最好的。不过我没明白为什么这里只比较了 BLH, OLH 和 RAPPOR,而不比较其他的方法。
Related Work
Related Work 介绍了一些当前的方法,其实挺值得一看的。
Discussion
这里又提了一下 answering multiple questions 的问题,传统来说 $\epsilon$ 被分到了不同的属性上面。这里作者说建议把用户分为许多组,每组用户单独回答一个属性的结果。即假设有 $Q \ge 2$ 个属性,那么相当于收集到的数据只有 $n/Q$ 了。在OLH中,方差是 $\sigma^{2}=\operatorname{Var}^{*}\left[\tilde{c}_{\mathrm{OLH}}(i) / n\right]=\frac{4 e^{\varepsilon}}{\left(e^{\varepsilon}-1\right)^{2} \cdot n}$了。
在给用户分组的情况下,相当于只有 $n/Q$ 的用户回答指定的问题,所以方差为 $\sigma_{1}^{2}=\frac{4 Q e^{\varepsilon}}{\left(e^{\varepsilon}-1\right)^{2} \cdot n}$,在将 $\epsilon$ 均分的情况下,用户量还是 $n$ ,但是epsilon变了,方差为 $\sigma_2^2=\frac{4 e^{\varepsilon / Q}}{\left(e^{\varepsilon / Q}-1\right)^{2} \cdot n}$,我们有:
上式中,第一项永远大于0的,为了化简第二项,令 $e^{\varepsilon / Q}=z$,则为:
也就是说,给用户分组比给隐私预算分配这个举措更加合理。
Limitations. 本文是在 pure LDP 的范畴下,那么当一个方法不是pure的时候,就不好用这个框架去分析了。另外,我们的数据假定是有界的,那么对于无界的数据,目前怎么处理还未知。
Conclusion
本文研究了LDP下频率估计的问题,首先提出了一个 pure LDP 的框架,并在此框架下分析了多重编码方法及其优化方法。同时给出了应用中的方法选择知道。
附录-额外的实验
本节测试了更多的实验。
Effect of Cohort Size

首先测试了RAPPOR不同配置的影响,如上图所示。
Performance on Synthetic Datasets
接着测试了不同生成数据集下不同试验参数的影响。比较的是BLH, OLH 和 RAPPOR。

Performance on Rockyou Dataset
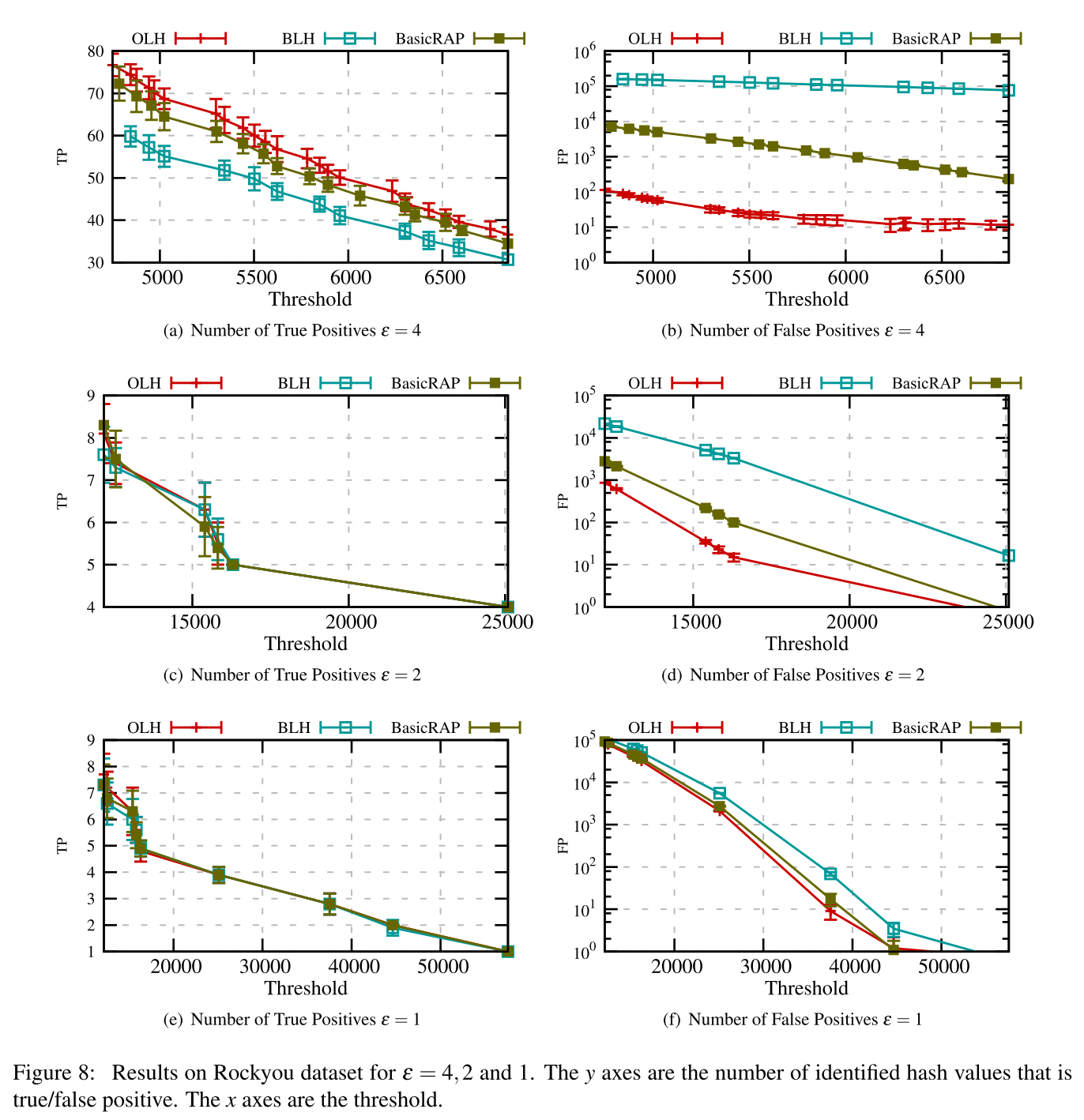
最后,作者找了一个叫做 Rockyou 的数据集,并在这个数据集上运行了不同的方法进行对比。实验结果大同小异。
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


